Kelvin Generator for electric fence, an example of a Luddite technology

Here is something I wrote about 5 years ago, when I was living in Arkansas, and modified it to enter the archdruid post-industrial technology contest.

Electric Fence Powered by Falling Water, with No Moving Parts

Motivation

We live in a wilderness area. Most of the year we can’t drive a vehicle here and it takes about an hour to an hour and a half to walk from the little country road to our place here in the valley. Our garden is surrounded by deer and bear habitat. We wanted to discourage them from entering our garden. 

We wanted to minimize buying anything for this fence, first because hardware is hard to carry in, and second because we wanted to figure out how to reuse what we have so as not to produce more waste. We also wanted to show by example how a balance can be struck between local consumption and local production, so as to contribute to the interdependent web of meaningful work existent in a local economy. An additional motivation was to see if such a traditionally high technology as a high voltage technology could be built in a de-industrialized setting. 

We have a lot of used metal and lots of water from a spring. It occurred to me that a Kelvin Generator might be the answer, and indeed it has been a success in keeping out bear and deer.

Description and design of Kelvin Generator

The generator, invented by Lord Kelvin many years ago, uses no mechanical or electronic parts. It converts gravitational potential energy of water into electrical energy: tens of thousands of volts with minimal bursts of current when discharged by an animal or person. The low current makes it ideal for a non-lethal shock, which would discourage but not kill animals or people. It uses the principle of positive feedback: any charge imbalance caused by thermal or quantum fluctuations in the water droplets is amplified by the way the parts are related/connected together. It consists of a container filled with water at the top (where county or city water is available, a direct connection, through a garden hose, to a pressurized source is also possible), metal pipes with a T (non-conductive pipe with wire inserted will work as well), two metal cylinders called charge inducers(bottomless tobacco cans were used) through which the water drips, two bottom metal containers into which the water falls under the inducers(washtubs were used), two metal wires cross-connecting the bottom containers to the inducers, and mechanical supports (fishing line hanging from branches or wooden framing) for the metal cans and wires (see Figure 1 for schematic, framing and fishing line supports not shown, Figure 2 for picture). 

To understand in more details how it works, one needs a rudimentary understanding of electrostatics, how metals distribute charge over their surface, how (opposite) charge can be induced across an insulative medium like air, and then follow a little charge imbalance in one of the droplets into the tub, through the cross wire, inducing the other stream droplets, into the other tub and back to the original stream through the other cross wire. As charged droplets fall into the tubs on the right side, charge redistributes to the inducers on the left side, creating more (opposite) charge on the left side droplets, which increase the charge on the left side tubs, redistributing to the right side inducers, which induce more charge on the right side droplets(etc.), until leakage of charge occurs and limits the voltage from rising any further. The main leakage paths are corona discharge through the air, conduction through weeds, and droplets hitting the sides of the inducers or wires. The top reservoir remains neutral because equal and opposite charge flows  through the metal pipes (or plastic pipes with metal wire) to droplets. The conductive path to/from the reservoir is broken once the droplets form while they fall (further separating).

For the top tank I used a used 55 gallon plastic (metal can also be used)drum with a hole drilled at the top where an input garden hose could fit. For drippers I used plastic tubing in combination with river cane reeds and hose clamps to limit the flow. I have also used industrial shower heads for greater flow in a situation when more pressure was available. We had two galvanized wash tubs, to be used as the bottom containers, and for the inducers I used two tin tobacco cans with their bottoms taken out. These were supported by fishing lines hanging from the metal pipes and by standard electric fence insulator supports, nailed to trees. The fishing line was used because of its high electrical resistance.

The washtubs have drain holes at the bottom. These can be adjusted relative to the flow rate from the drippers so that water leaks out so as not to accumulate water in the tubs (they would become too heavy) and yet to have a drip (as opposed to a conductive stream) to the ground. The physics of Faraday cages ensures that water can drip down to the ground, but no charge. Instead of letting the water fall to the ground and get wasted, I let them fall into irrigation tanks which were hooked up with hoses to a drip irrigation system, thus getting a second use from the water.

The fence needs to have two parts which do not touch. Each tub can have a fence wire conncted to it, then the fence wraps around the garden, terminating in two parts which can be separated by a gate, which is not itself connected to the electrified fence.

The following engineering tradeoffs were observed:

The diameter of the inducers needs to be small enough so that the electric field is large enough at the center near top and bottom in order for efficient induction to happen, and the capacitance between forming droplets and the inducers is thus large. But this capacitance also needs to be kept small because the saturation voltage is inversely proportional to its square root (see below for a mathematical understanding of the tradeoffs for this capacitance). The diameter of the inducers needs to be large enough so that droplets do not hit the sides as they fall down through it. 

The height of the inducers needs to be large enough so that the stream coming from the drippers has a chance to break up into droplets somewhere within an inch or so from the top and bottom (the electric field is weak inside the inducers but strong close to top and bottom). The length of the inducers needs to be small enough so droplets do not hit the sides as they stray off the centerline due to the electric fields.

The distance between the tubs/wires/inducers of opposite polarity needs to be large enough so that droplets straying off axis do not hit wires/tubs of opposite polarity, thus discharging the generator.  Also, the larger the distance between the tubs, the bigger fraction of the charge on the tub/inducer system is concentrated around the inducer, helping to prime the generator. The distance needs to be small enough to conserve space and piping material.

During the initial priming stage, the vertical distance between the drippers and top of the washtubs needs to be small enough to catch the droplets that move off axis due to electric fields, small initial deviations (which get amplified just from geometry) and wind. After the initial priming stage, once a high voltage is achieved, the vertical distance needs to be large enough for droplets to have enough momentum to fall into the tub under the influence of the (repulsive) electric field which pushes them off axis and away from the tub.

The diameter of the tubs needs to be large enough to catch the droplets, yet small enough to save on materials (if one is building the tubs) or practical enough to find tubs of that diameter.

The flow rate needs to be large enough to make the generator robust to small leakage (mostly from weeds, especially when starting to charge or after a zap/discharge). See below for a mathematical understanding of this. The flow rate needs to be small enough to save on water.

Assuming basic circuit physics, a negligible capacitance between each tub and ground, a parasitic resistance R2 between the electrodes (infinite initially, but see below), a capacitance C between a forming droplet and an inducer (equal to the capacitance between the inducer and ground, since the droplet is grounded by the stream above it just before it separates), a capacitance C’ between each inducer and the tub underneath, a capacitance C” between the two tubs, a flow of J charged droplets per second into a tub and a resistance R due to weed load and humidity between each tub/inducer/fence and ground, the initial voltage on the fence would be:

V=K*Exp[B*t],

where K is the initial charge fluctuation on a droplet (a few electrons of charge), t is the time and

B=(C*J-1/Reff)/(C+4*C’+2*C”),

Where 1/Reff=1/R+2/R2

The only term that makes this a generator rather than a capacitor is the C*J term, which acts like a negative conductance. 1/B is the time it would take to amplify the initial tiny voltage (due to statistical fluctuations of the charge on all the droplets leaving the stream at one time) by a factor of e(about 2.7). It can be shown that 1/B will be larger that the time between the droplets (1/J), but it can’t be much larger, or else the generator won't work, because an opposite charge fluctuation is likely to occur before induction and amplification takes over. So to keep B large (1/B small), the parasitic capacitances C' and C” have to be kept small.

If there was no conduction between the two electrodes, and if all the charged droplets fell into the tubs below, the voltage would either increase or decrease exponentially depending on whether C*J > 1/Reff, or C*J < 1/Reff, so in order for amplification to happen, the product of the capacitance between the ring and stream above (C) and the number of droplets per second (J) should be larger than 1/Reff. As the voltage increases, the infinite resistance R2 between the electrodes decreases due to droplets hitting oppositely charged conductors (which was not taken into account in the above equations), and so the effective resistance Reff decreases. J also decreases because some droplets no longer make it into the tub, and eventually the voltage reaches a saturation point when C*J=1/Reff. A way to understand the saturation voltage in the idealized case when 1/Reff=0, is to realize that the gravitational plus initial kinetic energy of a droplet is converted to kinetic energy as it falls, but also to electostatic potential energy as it climbs up an electrostatic potential towards the tub. At the idealized saturation voltage, all the initial energy will be converted to electostatic potential energy with no kinetic energy left (J=0) and the droplet will never reach the tub (in reality, it doesn't just hover. Any small initial momentum sideways, will be amplified by the electrostatic potential between the tubs, and the droplet will be deflected towards the other tub, or attempt to go back towards the ring in a beautiful upside down fountainlike effect). The idealized saturation voltage thus depends on the pressure exiting the dripper, and the height of the dripper above the tub. Assuming that all the gravitational energy of a droplet gets converted to electrostatic energy, and that there is no load (due to weeds or corona discharge) or parasitic resistance, the idealized saturation voltage Vmax would be roughly:

Vmax=(1/2*v_i^2+g*h)/rho, where v_i is the initial speed of a droplet as it comes out  of the dripper (which is proportional to the pressure in the top tank), g is the gravitational acceleration, h is the height of the bottom of the dripper relative to the top of the tub, and rho is  the charge of a droplet divided by the mass of a droplet. 

When the initial velocity of a droplet is negligible, the previous equation can also be written in terms of the capacitance C as: 

Vmax=(1/2*v_i^2+g*h)/rho, where v_i is the initial speed of a droplet as it comes out  of the dripper (which is proportional to the pressure in the top tank), g is the gravitational acceleration, h is the height of the bottom of the dripper relative to the top of the tub, and rho is  the charge of a droplet divided by the mass of a droplet. 

When the initial velocity of a droplet is negligible, the previous equation can also be written in terms of the capacitance C as:

Vmax=Sqrt[2*m*g*h/C], where m is the mass of a droplet.

These two equations are fertile ground for dripper engineering. Bigger droplets with less charge, more water in the top tank, bigger height of dripper relative to bottom tub, and smaller capacitance between inducer and droplet produce a larger saturation voltage.

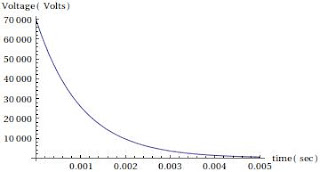
An attempt to model these effects in Mathematica produced figure 3, assuming the following dependence on voltage (V) for R2 and J:

R2[V] := a/(V) + Rmin

J[V] := J0*(1 - V/Vmax),

and the following numerical values (resistances in ohms, capacitances in farads):

a = 100000 (volts), Rmin = 1000000, J0 = 10/second,Vmax = 100000 Volts, c = 10^(-8), c’ = 10^(-12), c” = 10^(-12), K= 10^(-12), R = 10^(8).
If a zap occurs through an animal with a resistance R=10^5 ohms, then a discharge looking like Figure 4 occurs. Figure 5 is a plot of the current through the animal in such a zap. The current seems too large (since it didn't kill those zapped by it, including me), probably because the real C is smaller than 10 nano farads, and/or Vmax is smaller than 10^5 Volts. Figure 6 is a circuit diagram, trying to model the distributed system in a discrete way. The rectangles with squiggly lines are my symbol for a negative, voltage dependent resistor (there might be a more standard symbol).

For a 600 ft fence, the generator takes a few seconds to charge to saturation after startup or a zap, as long as the animal zapped does not hold on to the fence. If it holds on, the fence will not charge. The time to charge is proportional to the length of the fence (which is proportional to the capacitance of the fence to ground, data not shown).

As with most feedback systems, when they work they are fairly insensitive to design parameters, once a certain operating range is reached. Suggested dimensions based on experience are shown in Figure 1. The range of flows experimented with are in the range of one pint (under conditions of low humidity and low weed load) to one gallon of water per minute (high humidity and/or high weed load). The high flow was used in conjunction with an industrial shower head, so lots of drips jets in parallel from each head. 

Possible improvements

Materials could be found to replace those gotten from the waste stream of industrial technology. For example, bamboo pipes can be used instead of plastic or metal pipes. An automated (negative feedback) way to stop water flow when the charge/voltage reaches a level sufficient for zapping, and to start the flow when the level drops sufficiently (from weeds or a zap) would help to conserve water. Such a mechanism would be based on something similar to a toilet bowl float, except the lever turning off the water valve on the top tank would be actuated by electrostatic instead of mechanical/gravitational forces that move a  toilet bowl float.

Figure 1

Figure 2

Figure 3

Figure 4

Figure 5

Figure 6